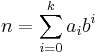Palindromic number
A palindromic number or numeral palindrome is a 'symmetrical' number like 16461, that remains the same when its digits are reversed. The term palindromic is derived from palindrome, which refers to a word like rotor that remains unchanged under reversal of its letters. The first palindromic numbers (in decimal) are:
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151, 161, 171, 181, 191, … (sequence A002113 in OEIS).
Palindromic numbers receive most attention in the realm of recreational mathematics. A typical problem asks for numbers that possess a certain property and are palindromic. For instance:
- The palindromic primes are 2, 3, 5, 7, 11, 101, 131, 151, … (sequence A002385 in OEIS).
- The palindromic square numbers are 0, 1, 4, 9, 121, 484, 676, 10201, 12321, … (sequence A002779 in OEIS).
Buckminster Fuller referred to palindromic numbers as Scheherazade numbers in his book Synergetics, because Scheherazade was the name of the story-telling wife in the 1001 Nights.
It is fairly straightforward to appreciate that in any base there are infinitely many palindromic numbers, since in any base the infinite sequence of numbers written (in that base) as 101, 1001, 10001, etc. (in which the nth number is a 1, followed by n zeros, followed by a 1) consists of palindromic numbers only.
Contents |
Formal definition
Although palindromic numbers are most often considered in the decimal system, the concept of palindromicity can be applied to the natural numbers in any numeral system. Consider a number n > 0 in base b ≥ 2, where it is written in standard notation with k+1 digits ai as:
with, as usual, 0 ≤ ai < b for all i and ak ≠ 0. Then n is palindromic if and only if ai = ak−i for all i. Zero is written 0 in any base and is also palindromic by definition.
Decimal palindromic numbers
All numbers in base 10 with one digit are palindromic. The number of palindromic numbers with two digits is 9:
- {11, 22, 33, 44, 55, 66, 77, 88, 99}.
There are 90 palindromic numbers with three digits (Using the Rule of product: 9 choices for the first digit - which determines the third digit as well - multiplied by 10 choices for the second digit):
- {101, 111, 121, 131, 141, 151, 161, 171, 181, 191, …, 909, 919, 929, 939, 949, 959, 969, 979, 989, 999}
and also 90 palindromic numbers with four digits: (Again, 9 choices for the first digit multiplied by ten choices for the second digit. The other two digits are determined by the choice of the first two)
- {1001, 1111, 1221, 1331, 1441, 1551, 1661, 1771, 1881, 1991, …, 9009, 9119, 9229, 9339, 9449, 9559, 9669, 9779, 9889, 9999},
so there are 199 palindromic numbers below 104. Below 105 there are 1099 palindromic numbers and for other exponents of 10n we have: 1999, 10999, 19999, 109999, 199999, 1099999, … (sequence A070199 in OEIS). For some types of palindromic numbers these values are listed below in a table. Here 0 is included.
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 1010 | |
| n natural | 10 | 19 | 109 | 199 | 1099 | 1999 | 10999 | 19999 | 109999 | 199999 |
| n even | 5 | 9 | 49 | 89 | 489 | 889 | 4889 | 8889 | 48889 | 88889 |
| n odd | 5 | 10 | 60 | 110 | 610 | 1110 | 6110 | 11110 | 61110 | 111110 |
| n square | 4 | 7 | 14 | 15 | 20 | 31 | ||||
| n cube | 3 | 4 | 5 | 7 | 8 | |||||
| n prime | 4 | 5 | 20 | 113 | 781 | 5953 | ||||
| n squarefree | 6 | 12 | 67 | 120 | 675 | 1200 | 6821 | 12160 | + | + |
| n non-squarefree (μ(n)=0) | 4 | 7 | 42 | 79 | 424 | 799 | 4178 | 7839 | + | + |
| n square with prime root | 2 | 3 | 5 | |||||||
| n with an even number of distinct prime factors (μ(n)=1) | 2 | 6 | 35 | 56 | 324 | 583 | 3383 | 6093 | + | + |
| n with an odd number of distinct prime factors (μ(n)=-1) | 4 | 6 | 32 | 64 | 351 | 617 | 3438 | 6067 | + | + |
| n even with an odd number of prime factors | 1 | 2 | 9 | 21 | 100 | 180 | 1010 | 6067 | + | + |
| n even with an odd number of distinct prime factors | 3 | 4 | 21 | 49 | 268 | 482 | 2486 | 4452 | + | + |
| n odd with an odd number of prime factors | 3 | 4 | 23 | 43 | 251 | 437 | 2428 | 4315 | + | + |
| n odd with an odd number of distinct prime factors | 4 | 5 | 28 | 56 | 317 | 566 | 3070 | 5607 | + | + |
| n even squarefree with an even number of (distinct) prime factors | 1 | 2 | 11 | 15 | 98 | 171 | 991 | 1782 | + | + |
| n odd squarefree with an even number of (distinct) prime factors | 1 | 4 | 24 | 41 | 226 | 412 | 2392 | 4221 | + | + |
| n odd with exactly 2 prime factors | 1 | 4 | 25 | 39 | 205 | 303 | 1768 | 2403 | + | + |
| n even with exactly 2 prime factors | 2 | 3 | 11 | 64 | 413 | + | + | |||
| n even with exactly 3 prime factors | 1 | 3 | 14 | 24 | 122 | 179 | 1056 | 1400 | + | + |
| n even with exactly 3 distinct prime factors | 0 | 1 | 18 | 44 | 250 | 390 | 2001 | 2814 | + | + |
| n odd with exactly 3 prime factors | 0 | 1 | 12 | 34 | 173 | 348 | 1762 | 3292 | + | + |
| n Carmichael number | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| n for which σ(n) is palindromic | 6 | 10 | 47 | 114 | 688 | 1417 | 5683 | + | + | + |
Perfect powers
There are many palindromic perfect powers nk, where n is a natural number and k is 2, 3 or 4.
- Palindromic squares: 0, 1, 4, 9, 121, 484, 676, 10201, 12321, 14641, 40804, 44944, ... (sequence A002779 in OEIS)
- Palindromic cubes: 0, 1, 8, 343, 1331, 1030301, 1367631, 1003003001, ... (sequence A002781 in OEIS)
- Palindromic fourth powers: 0, 1, 14641, 104060401, 1004006004001, ... (sequence A186080 in OEIS)
No palindromes of form n5 (or higher exponent) have been found. The only known non-palindromic number, whose cube is a palindrome, is 2201.
G. J. Simmons conjectured there are no palindromes of form nk for k > 4.[1]
Other bases
Palindromic numbers can be considered in other numeral systems than decimal. For example, the binary palindromic numbers are:
- 0, 1, 11, 101, 111, 1001, 1111, 10001, 10101, 11011, 11111, 100001, …
or in decimal: 0, 1, 3, 5, 7, 9, 15, 17, 21, 27, 31, 33, … (sequence A006995 in OEIS). The Mersenne primes form a subset of the binary palindromic primes.
All numbers are palindromic in an infinite number of bases. But, it's more interesting to consider bases smaller than the number itself - in which case most numbers are palindromic in more than one base.
In base 18, some powers of seven are palindromic:
73 = 111 74 = 777 76 = 12321 79 = 1367631
And in base 24 the first eight powers of five are palindromic as well:
51 = 5 52 = 11 53 = 55 54 = 121 55 = 5A5 56 = 1331 57 = 5FF5 58 = 14641 5A = 15AA51 5C = 16FLF61
Any number n is palindromic in all bases b with b ≥ n + 1 (trivially so, because n is then a single-digit number), and also in base n−1 (because n is then 11n−1). A number that is non-palindromic in all bases 2 ≤ b < n − 1 is called a strictly non-palindromic number.
Lychrel process
Non-palindromic numbers can be paired with palindromic ones via a series of operations. First, the non-palindromic number is reversed and the result is added to the original number. If the result is not a palindromic number, this is repeated until it gives a palindromic number.
It is not known whether all non-palindromic numbers can be paired with palindromic numbers in this way. While no number has been proven to be unpaired, many do not appear to be. For example, 196 does not yield a palindrome even after 700,000,000 iterations. Any number that never becomes palindromic in this way is known as a Lychrel number.
Sum of the Reciprocals
The sum of the reciprocals of the palindromic numbers is a convergent series, whose value is approximately 3.37028... (sequence A118031 in OEIS).
See also
Notes
References
- Malcolm E. Lines: A Number for Your Thoughts: Facts and Speculations about Number from Euclid to the latest Computers: CRC Press 1986, ISBN 0852744951, S. 61 (Limited Online-Version (Google Books))